9° Aplicación de la Ecuación de una recta

Ejercicio

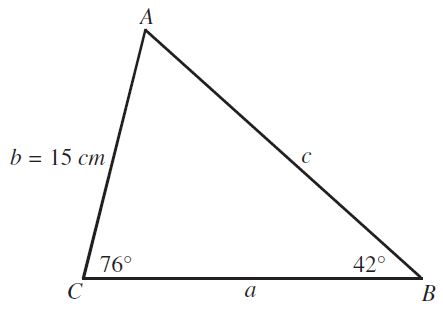
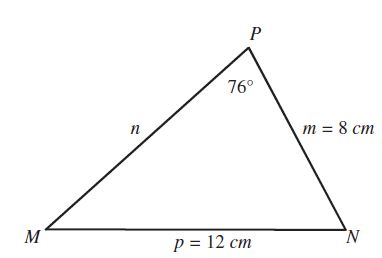
• Los siguientes ejercicios resolverlos en hojas y entregarlos en el siguiente en el siguiente encuentro.

*La ecuación de la recta que pasa por

1. el punto A= (-4, -3)  y que tiene una pendiente de m= 2 
2. el punto A= (-3, -2)  y que tiene una pendiente de m= 3
3. el punto A= (4, -3,5)  y que tiene una pendiente de m= 1,5 
4. el punto A= (-4,2, 3,1)  y que tiene una pendiente de m= 2,3

9° La recta y su pendiente

LA RECTA

En geometría euclidiana, la recta o la línea recta se extiende en una misma dirección por tanto tiene una sola dimensión y contiene infinitos puntos; se puede considerar que está compuesta de infinitos segmentos. Dicha recta también se puede describir como una sucesión continua e indefinida de puntos extendidos en una sola dimensión, es decir, no posee principio ni fin.

Ecuación de la recta en el plano

En un plano cartesiano, podemos representar una recta mediante una ecuación general definida en dicho plano ya sea mediante coordenadas usando puntos y vectores, o bien funciones que especifican dichas coordenadas.

Ecuación general de la recta

La ecuación general de una recta esta dada por la expresión: 

con  y ,¹⁰ , donde  representa la pendiente de la recta y  señala la ordenada en el origen, datos suficientes para representar cualquier recta en el plano cartesiano.

• Pendiente y ordenada al origen

Dada una recta mediante un punto, ${\displaystyle P=(x_{0},y_{0})\,}$, y una pendiente ${\displaystyle m\,}$:

Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente (ecuación punto-pendiente):

${\displaystyle y-y_{0}=m(x-x_{0})\!}$

donde ${\displaystyle m}$ es la tangente del ángulo que forma la recta con el eje de abscisas X.

Forma simplificada de la ecuación de la recta

• Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas es (0, b), podemos deducir, partiendo de la ecuación general de la recta, ${\displaystyle y-y_{1}=m(x-x_{1})}$:

  ${\displaystyle y-b=m(x-0)\!}$ ${\displaystyle y-b=mx\!}$ ${\displaystyle y=mx+b\!}$ Ejemplo La ecuación de la recta que pasa por el punto  y que tiene una pendiente de  es: Sustituyendo en la ecuación anterior tenemos: ${\displaystyle y-y_{1}=m(x-x_{1})\!}$ ${\displaystyle y-(-8)=2(x-(-8))\!}$ ${\displaystyle y+8=2(x+8)\!}$ ${\displaystyle y+8=2x+16\!}$ ${\displaystyle y-2x+8-16=0\!}$ ${\displaystyle y-2x-8=0\!}$

  
  

11° Función cuadrática

Función cuadrática, graficar parábola

En el siguiente video podran reformar el tema de función cuadrática, y los pasos a seguir para poder graficarla.

https://www.youtube.com/watch?v=ira6fc3zuRg

6° Polinomios aritmeticos

Los siguientes ejercicios resolverlos y entregarlos el próximo encuentro en hojas cuadriculadas.

Un polinomio Aritmético es una expresión que combina las cuatro operaciones básicas.

1. 

2.

3.

4.

8° Factorización

Los siguientes ejercicios resolverlos en hojas cuadriculadas y presentarlos en el próximo encuentro.

Factorizar

1x³ + x²

22x⁴ + 4x²

3x² − 4

4x⁴ − 16

59 + 6x + x²

10° Teorema del Seno y coseno

Los siguientes ejercicios son el refuerzo al tema Teorema del Seno y poder continuar con el Teorema del Coseno. por favor estudiar y poner en práctica de forma autónoma 

el video.

Ley del Seno:

 1. Dado ∆ABC con A = 30°, B = 20° y a = 45 m. Encuentre el ángulo y los lados faltantes.

     

2. Dado A = 42°, B = 75° y c = 22 cm. Encuentre el ángulo y los lados faltantes.

3. Dado a = 22, b =12 y A = 40°. Encuentre los otros ángulos y el lado.

Fórmula para la Ley de Cosenos

La fórmula será la siguiente:

1.- En el siguiente triángulo ABC, a = 13 cm, c = 19 cm, <B = 55° , Resuelva el triángulo.

10° Teorema o ley del seno

Resuelve los siguientes ejercicios y entregalos en la siguiente sesión en hojas cuadriculadas.

La fórmula para resolver ejercicios de triángulos mediante la ley de senos, es la siguiente:

1. En el triángulo  ABC, b = 15 cm, <B = 42°, y <C = 76°. Calcula la medida de los lados y ángulos restantes.

2. Calcula los lados y el ángulo que falta en el siguiente triángulo oblicuángulo.

3. Calcula los lados y el ángulo que falta en el siguiente triángulo oblicuángulo.

4. Calcula el lado y los ángulos que faltan del siguiente triángulo oblicuángulo.